En esencia, una prensa hidráulica funciona según un principio fundamental de la mecánica de fluidos conocido como Ley de Pascal. Este principio establece que cualquier presión aplicada a un fluido confinado e incompresible se transmite sin disminución a cada porción del fluido y a las paredes de su contenedor. Esta sencilla regla permite a una prensa hidráulica lograr una increíble multiplicación de la fuerza.
La idea central es que un sistema hidráulico no multiplica la presión, sino la fuerza . Al transmitir una presión constante desde un área pequeña a otra mucho mayor, una fuerza de entrada pequeña puede generar una fuerza de salida enorme.

¿Qué es la ley de Pascal?
La Ley de Pascal es el concepto fundamental que rige la hidrostática y la potencia de los sistemas hidráulicos. Comprenderla es clave para entender cómo funcionan estas máquinas.
El principio básico: presión uniforme
La ley, articulada por primera vez por Blaise Pascal, dicta que cuando se produce un aumento de presión en cualquier punto de un fluido confinado, se produce un aumento igual en todos los demás puntos de ese recipiente.
Imaginemos el fluido como un medio que transmite la presión perfectamente y por igual en todas direcciones.
Una analogía intuitiva
Piense en una botella de agua de plástico cerrada. Si aprietas una parte de la botella, todo el recipiente se vuelve firme. La presión que ejerces con el pulgar no sólo se siente bajo el pulgar, sino que se transmite a toda el agua, presionando por igual en todas las superficies interiores de la botella.
El mecanismo de multiplicación de fuerzas
La Ley de Pascal por sí sola no es más que un principio. Su poder se despliega cuando se combina con la relación entre presión, fuerza y área.
La fórmula crítica: Presión = Fuerza / Área
Presión ( P ) se define como la cantidad de fuerza ( F ) aplicada perpendicularmente sobre un área específica ( A ). Esta sencilla ecuación P = F/A es la clave matemática de la prensa hidráulica.
Reajustando la fórmula a F = P x A se puede ver que, para una presión dada, un área mayor producirá una fuerza mayor.
Cómo aprovecha esto la prensa
Una prensa hidráulica utiliza dos pistones conectados de diferentes tamaños con un fluido confinado (normalmente aceite) entre ellos.
Se aplica una pequeña fuerza al pistón pequeño de "entrada". Esto genera una cantidad específica de presión en el fluido (P = F₁/A₁).
El resultado: Fuerza de salida amplificada
Debido a la Ley de Pascal, esta misma presión se transmite a través del fluido al pistón grande de salida.
En el pistón de salida, esta presión actúa sobre un área mucho mayor. Esto produce una fuerza de salida proporcionalmente mayor ( F₂ = P x A₂ ). Si el pistón de salida tiene 100 veces el área del pistón de entrada, obtendrá 100 veces la fuerza de salida.
Comprender las compensaciones
Esta extraordinaria multiplicación de la fuerza no surge de la nada, sino que obedece a las leyes de la física, que siempre exigen una compensación.
El principio de "no comer gratis": trabajo y distancia
El sistema no crea energía gratuita. El trabajo realizado en el pistón de entrada (Fuerza x Distancia) debe ser igual al trabajo realizado por el pistón de salida (sin tener en cuenta las pequeñas pérdidas por fricción).
Para generar una gran fuerza de salida en una distancia corta, debes aplicar una pequeña fuerza de entrada en una distancia mucho más larga. mayor distancia . Se intercambia una mayor distancia de desplazamiento en el pistón pequeño por una mayor fuerza en el pistón grande.
El papel del fluido
Todo este proceso depende de que el fluido sea incompresible . Los líquidos como el aceite son ideales porque no se comprimen fácilmente bajo presión, lo que garantiza una transmisión eficaz de la fuerza.
Si se utilizara un gas compresible como el aire (un sistema neumático), la fuerza de entrada se desperdiciaría primero en comprimir el aire antes de poder mover eficazmente el pistón de salida.
Aplicación de estos conocimientos
Comprender este principio es útil tanto para estudiantes como para ingenieros o técnicos.
- Si tu objetivo principal es el diseño de ingeniería: La relación entre las áreas de los pistones es el factor más importante que determina el factor de multiplicación de la fuerza de la máquina.
- Si su principal interés es la teoría física: La conservación de la energía se sustenta en el equilibrio entre fuerza y distancia; el trabajo de entrada es igual al trabajo de salida.
- Si su principal interés es el funcionamiento práctico: La integridad del sistema es primordial. Cualquier fuga rompe la condición de "fluido confinado", y cualquier burbuja de aire reducirá drásticamente la eficiencia al introducir compresibilidad.
Aprovechando un sencillo principio de fluidos, la prensa hidráulica transforma con elegancia un pequeño empuje en una inmensa potencia.
Cuadro sinóptico:
| Aspecto | Detalle clave |
|---|---|
| Principio | Ley de Pascal: La presión en un fluido confinado se transmite por igual en todas las direcciones. |
| Mecanismo | Multiplicación de fuerzas mediante pistones de áreas diferentes (F = P × A). |
| Contrapartida | Fuerza de entrada aplicada en una distancia mayor a cambio de una fuerza de salida mayor en una distancia menor. |
| Requisitos del fluido | Fluido incompresible (por ejemplo, aceite) para una transmisión eficaz de la fuerza. |
Mejore las capacidades de su laboratorio con las prensas hidráulicas avanzadas de KINTEK. Tanto si realiza ensayos de materiales, preparación de muestras o experimentos de compresión, nuestras prensas de laboratorio automáticas, prensas isostáticas y prensas de laboratorio calefactadas ofrecen un control preciso de la fuerza y fiabilidad. No deje que la ineficacia le frene. póngase en contacto con nosotros para hablar de cómo nuestras soluciones pueden aumentar su productividad y precisión en el laboratorio.
Guía Visual
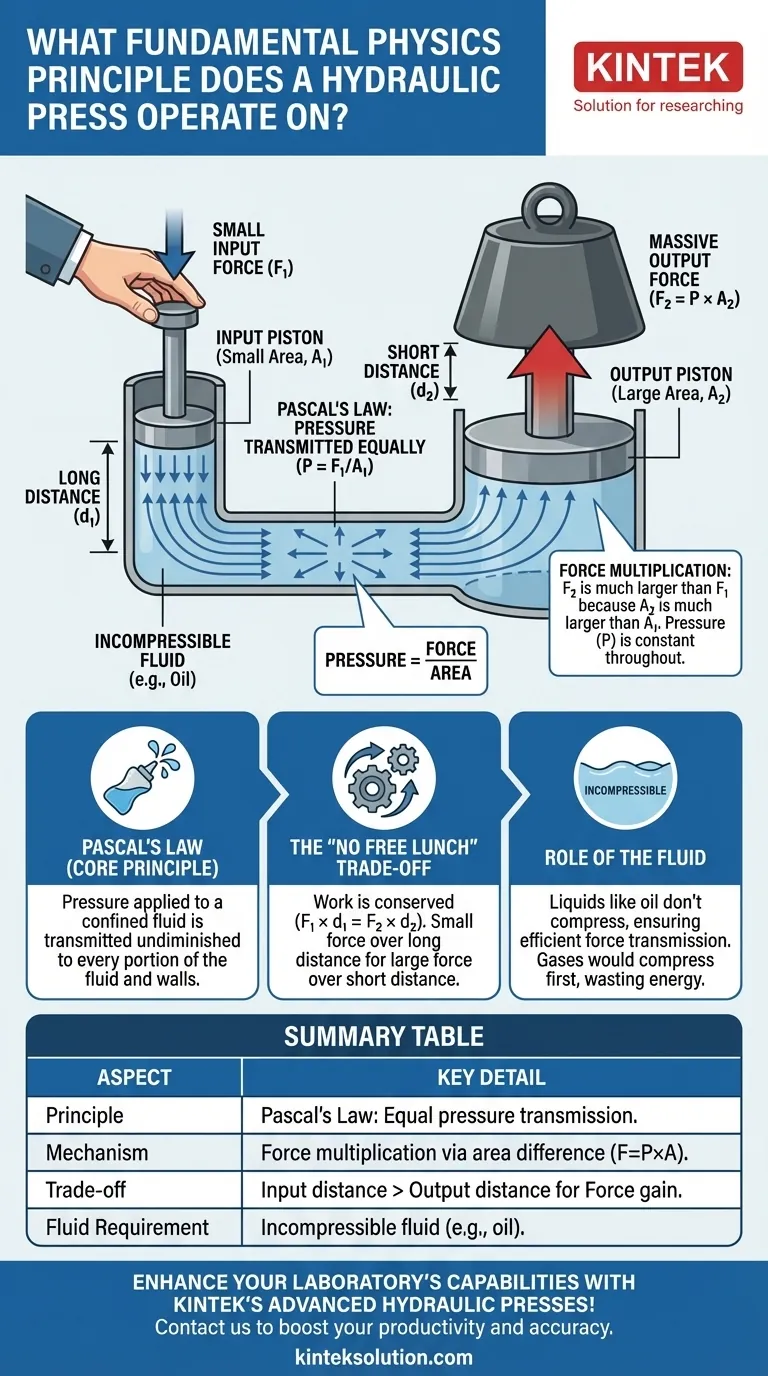
Productos relacionados
- Prensa hidráulica de laboratorio 2T Prensa de pellets de laboratorio para KBR FTIR
- Prensa hidráulica de laboratorio Prensa para pellets de laboratorio Prensa para pilas de botón
- Prensa hidráulica automática de laboratorio para prensado de pellets XRF y KBR
- Automática de laboratorio de prensa hidráulica de pellets de laboratorio de prensa de la máquina
- Prensa hidráulica de laboratorio manual calentada con placas calientes integradas Máquina prensa hidráulica
La gente también pregunta
- ¿Cómo se utiliza una prensa hidráulica de laboratorio para muestras de FT-IR de Marco Orgánico de Tb(III)? Guía Experta para la Preparación de Pastillas
- ¿Cuál es el papel de una prensa hidráulica en la preparación de pastillas de KBr para FTIR? Logre información química de alta resolución
- ¿Qué papel juega una prensa hidráulica de laboratorio en la preparación de polvo de carbonato? Optimice el análisis de su muestra
- ¿Por qué es crucial la uniformidad de la muestra al usar una prensa hidráulica de laboratorio para pellets de KBr de ácido húmico? Logre precisión FTIR
- ¿Cómo se utiliza una prensa hidráulica de laboratorio en la caracterización FT-IR de nanopartículas de sulfuro de cobre?



















