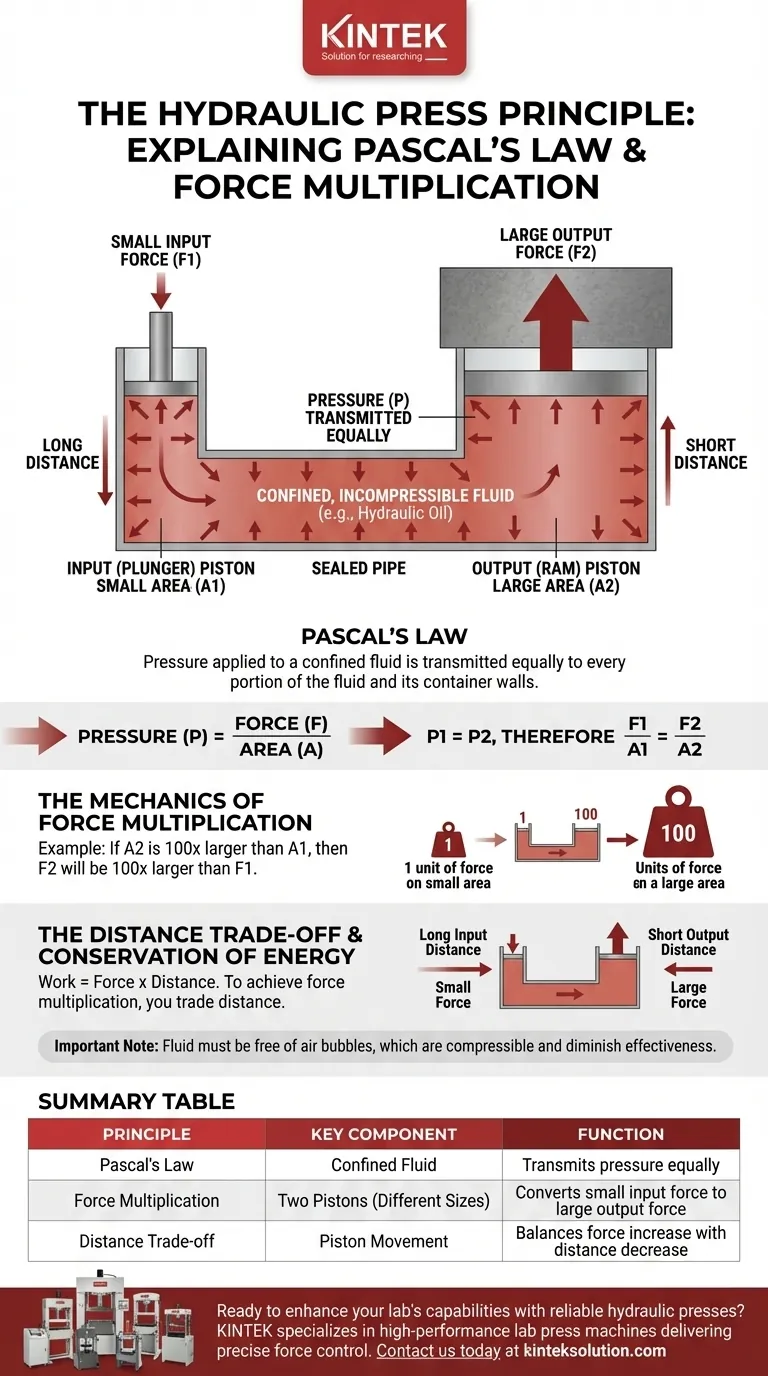
El principio fundamental de una prensa hidráulica es la Ley de Pascal. Esta ley científica establece que la presión aplicada a un fluido cerrado e incompresible se transmite por igual y sin disminuir a cada porción del fluido y a las paredes de su contenedor. Esto permite que una pequeña fuerza de entrada en un área pequeña se convierta en una fuerza de salida masiva en un área mayor.
La idea central no es que una prensa hidráulica cree fuerza de la nada, sino que multiplica la fuerza por la distancia de intercambio. Una fuerza pequeña aplicada sobre una distancia larga en un pistón pequeño genera una fuerza enorme sobre una distancia corta en un pistón grande.
La ley de Pascal
Para entender cómo funciona una prensa hidráulica, primero debe comprender los dos conceptos clave de la Ley de Pascal: la presión y un fluido confinado.
¿Qué es un fluido confinado?
Un sistema hidráulico utiliza un fluido (normalmente aceite) en un circuito cerrado y sellado. Esto es fundamental porque los líquidos son en gran medida incompresibles .
A diferencia del aire en un globo, no se puede comprimir fácilmente un volumen de aceite en un espacio más pequeño. Esta propiedad garantiza que cualquier fuerza que se aplique se transmita directamente, sin desperdiciarse en comprimir el propio fluido.
La presión se transmite por igual
La Ley de Pascal dicta que si se aumenta la presión en cualquier punto de este fluido confinado, la presión aumenta en la misma cantidad en todas partes del sistema.
Piense en apretar una bolsa de plástico sellada llena de agua. La presión que ejerces con los dedos no sólo se siente directamente debajo de ellos, sino que se distribuye por toda la superficie interior de la bolsa.
La mecánica de la multiplicación de fuerzas
La verdadera potencia de una prensa hidráulica proviene de la explotación de esta presión uniforme a través de dos pistones de diferentes tamaños.
El sistema de dos pistones
El sistema hidráulico más sencillo consta de dos cilindros, cada uno con un pistón, conectados por una tubería. Un cilindro es estrecho (el pistón de entrada o "émbolo") y el otro es ancho (el pistón de salida o "ariete").
Todo el sistema está lleno de fluido hidráulico.
La fórmula gobernante: Presión = Fuerza / Área
La presión (P) se define como la fuerza (F) aplicada sobre un área específica (A). La ecuación es P = F / A .
Como la Ley de Pascal dice que la presión es la misma en todo el fluido, la presión en el pistón pequeño (P1) es igual a la presión en el pistón grande (P2).
Esto nos da la ecuación maestra F1 / A1 = F2 / A2 .
Cómo una fuerza pequeña crea una fuerza grande
Esta ecuación revela el secreto. Supongamos que el pistón grande (A2) tiene una superficie 100 veces mayor que el pistón pequeño (A1).
Para mantener el equilibrio de la ecuación, la fuerza ejercida por el pistón grande (F2) debe ser 100 veces mayor que la fuerza aplicada al pistón pequeño (F1).
Aplicando una fuerza pequeña y manejable al pistón pequeño, se genera una fuerza inmensa y multiplicada en el pistón grande, capaz de aplastar coches o dar forma al acero.
Comprender las compensaciones
Esta multiplicación de fuerzas no viola las leyes de la física. No se obtiene "energía gratis"; simplemente se hace una compensación.
Conservación de la energía
El trabajo realizado en el pistón de entrada debe ser igual al trabajo realizado por el pistón de salida (sin tener en cuenta las pequeñas pérdidas por rozamiento). El trabajo se calcula como Trabajo = Fuerza x Distancia .
El ineludible "compromiso de distancia"
Para conseguir multiplicar la fuerza por 100 en nuestro ejemplo, hay que pagar un precio en distancia.
Para mover el pistón grande sólo 2,5 cm hacia arriba, debes empujar el pistón pequeño 30 cm hacia abajo. Se cambia una distancia larga de movimiento fácil por una distancia corta de movimiento potente.
La importancia del fluido
La elección del fluido no es arbitraria. Se utiliza aceite hidráulico porque es incompresible , lubrica las piezas móviles del sistema y es estable a altas temperaturas.
Lo más importante es que el sistema no contenga burbujas de aire. El aire es compresible y absorbería la fuerza aplicada, disminuyendo gravemente la eficacia de la prensa.
La elección correcta para su objetivo
Comprender el principio básico le permite ver cómo se aplica esta tecnología en todo tipo de aplicaciones, desde frenos de automóviles hasta maquinaria industrial.
- Si su objetivo principal es la física: La clave es ver cómo la Ley de Pascal (P = F/A) y la conservación del trabajo (Fuerza x Distancia) son los dos pilares que rigen todos los sistemas hidráulicos.
- Si su enfoque principal es la ingeniería o la mecánica: Recuerda que la eficacia del sistema depende del uso de un fluido realmente incompresible y de la maximización de la relación entre las áreas del pistón de salida y de entrada.
- Si su interés principal es el conocimiento general: Lo más sencillo es que los sistemas hidráulicos le permiten cambiar un empuje largo y fácil por uno corto e increíblemente potente.
Al manipular la fuerza y la distancia a través de un fluido, la prensa hidráulica hace posibles tareas monumentales con un esfuerzo de entrada mínimo.
Cuadro sinóptico:
| Principio | Componente clave | Función |
|---|---|---|
| Ley de Pascal | Fluido confinado | Transmite la presión por igual en un sistema sellado |
| Multiplicación de fuerzas | Dos pistones | Convierte una fuerza de entrada pequeña en una fuerza de salida grande |
| Compensación de distancias | Movimiento del pistón | Equilibra el aumento de la fuerza con la disminución de la distancia |
| Fluidos necesarios | Aceite hidráulico | Garantiza la incompresibilidad y la lubricación |
¿Está preparado para mejorar las capacidades de su laboratorio con prensas hidráulicas fiables? KINTEK está especializada en prensas de laboratorio de alto rendimiento, incluidas prensas de laboratorio automáticas, prensas isostáticas y prensas de laboratorio calefactadas, diseñadas para ofrecer un control preciso de la fuerza y durabilidad para sus necesidades de laboratorio. Nuestras soluciones le ayudan a realizar ensayos y procesar materiales de forma eficaz, ahorrando tiempo y mejorando los resultados. Póngase en contacto con nosotros para hablar de cómo nuestros equipos pueden ayudarle en sus aplicaciones específicas y aumentar su productividad.
