En esencia, la Ley de Pascal establece que un cambio de presión en cualquier punto de un fluido incompresible encerrado se transmite igual y sin disminuir a todas las porciones de ese fluido. Esto significa que si empujas un fluido en un recipiente sellado, la presión aumenta en todas partes dentro de ese recipiente exactamente en la misma cantidad, en el mismo momento exacto.
Si bien la definición se centra en la transmisión de presión, el verdadero poder de la Ley de Pascal reside en cómo nos permite lograr una gran multiplicación de la fuerza. Este único principio es la base de casi todos los sistemas hidráulicos modernos.
La Ecuación Fundamental: Presión, Fuerza y Área
Para comprender las implicaciones de la Ley de Pascal, primero debe comprender la relación entre sus tres componentes principales.
Definición de Presión
La presión (P) se define como una Fuerza (F) aplicada sobre un Área (A) específica. La ecuación es P = F/A.
Piense en la diferencia entre alguien que lo empuja con la palma abierta frente a un solo dedo. La fuerza puede ser la misma, pero la presión del dedo es mucho mayor porque se concentra en un área mucho más pequeña.
El Papel de un Fluido Incompresible
La Ley de Pascal se basa en el uso de un fluido incompresible, como el agua o el aceite hidráulico. Cuando aplica fuerza a este tipo de fluido, no se comprime en un volumen más pequeño.
Debido a que el fluido no se puede comprimir, la energía que introduce debe transmitirse a otro lugar. Así es como la presión se propaga instantáneamente por todo el sistema.
La Magia de la Multiplicación de Fuerza
El verdadero genio de aplicar la Ley de Pascal no es solo que la presión se transmite, sino que se puede aprovechar para multiplicar la fuerza. Este es el principio operativo detrás de todo, desde un gato hidráulico hasta el tren de aterrizaje de un avión.
El Modelo Hidráulico Básico
Imagine un tubo en forma de U lleno de aceite, sellado en ambos extremos por pistones. Un pistón es pequeño (el pistón de entrada) y el otro es grande (el pistón de salida).
Aplicación de la Fuerza de Entrada
Supongamos que aplica una pequeña fuerza descendente (F1) al pistón pequeño, que tiene un área de A1. Esto crea una presión en el fluido: P = F1 / A1.
Transmisión de la Presión
De acuerdo con la Ley de Pascal, esta presión exacta (P) está ahora presente en todas partes del fluido. Esto incluye el área directamente debajo del pistón de salida grande.
Cálculo de la Fuerza de Salida
Esta misma presión (P) ahora empuja hacia arriba sobre el pistón grande, que tiene un área de A2. La fuerza ascendente resultante (F2) es F2 = P x A2.
Dado que la presión es la misma en todas partes (F1/A1 = F2/A2), puede ver que la fuerza de salida es proporcional a la relación de las áreas. Si el área del pistón de salida es 10 veces mayor que el área del pistón de entrada, la fuerza de salida será 10 veces mayor que la fuerza que aplicó.
Comprensión de las Compensaciones (Trade-offs)
Esta multiplicación de fuerza no surge de la nada; sigue las leyes de la física e implica compromisos críticos.
Conservación de la Energía
No se puede crear energía de la nada. Si bien la fuerza de salida se multiplica, la distancia que se mueve el pistón de salida se reduce proporcionalmente.
Para elevar el pistón grande 1 pulgada, es posible que deba presionar el pistón pequeño hacia abajo 10 pulgadas. El trabajo realizado (Fuerza x Distancia) sigue siendo el mismo en ambos lados, ignorando la fricción.
La Importancia de un Sistema "Encerrado"
El principio de Pascal solo funciona en un sistema perfectamente sellado. Cualquier fuga provocará que el fluido escape cuando se aplica presión, disipando la presión y provocando fallas en el sistema.
Las Propiedades del Fluido Importan
Si bien a menudo asumimos un fluido ideal e incompresible, los fluidos hidráulicos del mundo real tienen viscosidad (resistencia al flujo) y pueden contener burbujas de aire atrapadas. El aire es altamente compresible, y su presencia en las líneas hidráulicas puede hacer que el sistema se sienta "esponjoso" y reducir drásticamente su eficiencia.
Cómo Aplicarlo a Su Proyecto
Comprender el principio le permite diseñar y solucionar problemas de sistemas de manera efectiva. Su objetivo específico determinará qué aspecto de la ley es más importante.
- Si su enfoque principal es la ventaja mecánica: Concéntrese en maximizar la relación de área entre los pistones de salida y de entrada (A2/A1) para lograr la multiplicación de fuerza deseada para una prensa o un gato elevador.
- Si su enfoque principal es la eficiencia del sistema: Dé prioridad a la creación de un sistema perfectamente sellado y al uso de un fluido incompresible de alta calidad para minimizar las pérdidas de energía por fugas o compresión interna.
- Si su enfoque principal es el control de precisión: Aproveche la compensación de trabajo; un movimiento pequeño y manejable en la entrada puede traducirse en un movimiento muy pequeño pero potente y preciso en la salida, lo cual es ideal para sistemas como los frenos de vehículos.
Al comprender este principio, usted pasa de simplemente conocer una definición a comprender el poder elegante detrás de toda la ingeniería hidráulica.
Tabla de Resumen:
| Aspecto | Conocimiento Clave |
|---|---|
| Definición | El cambio de presión en un fluido incompresible se transmite igual y sin disminuir. |
| Multiplicación de Fuerza | La fuerza de salida aumenta con la relación de área (F2 = F1 × (A2/A1)). |
| Compensaciones | El aumento de fuerza reduce la distancia de movimiento; la energía se conserva. |
| Aplicaciones | Se utiliza en gatos hidráulicos, prensas y sistemas de control de precisión. |
¿Listo para aprovechar la Ley de Pascal para las necesidades hidráulicas de su laboratorio? KINTEK se especializa en máquinas de prensas de laboratorio de alto rendimiento, incluidas prensas de laboratorio automáticas, prensas isostáticas y prensas de laboratorio calentadas. Nuestro equipo garantiza un control de fuerza preciso, durabilidad y eficiencia para sus aplicaciones de laboratorio. Contáctenos hoy para analizar cómo nuestras soluciones pueden optimizar sus proyectos e impulsar la productividad.
Guía Visual
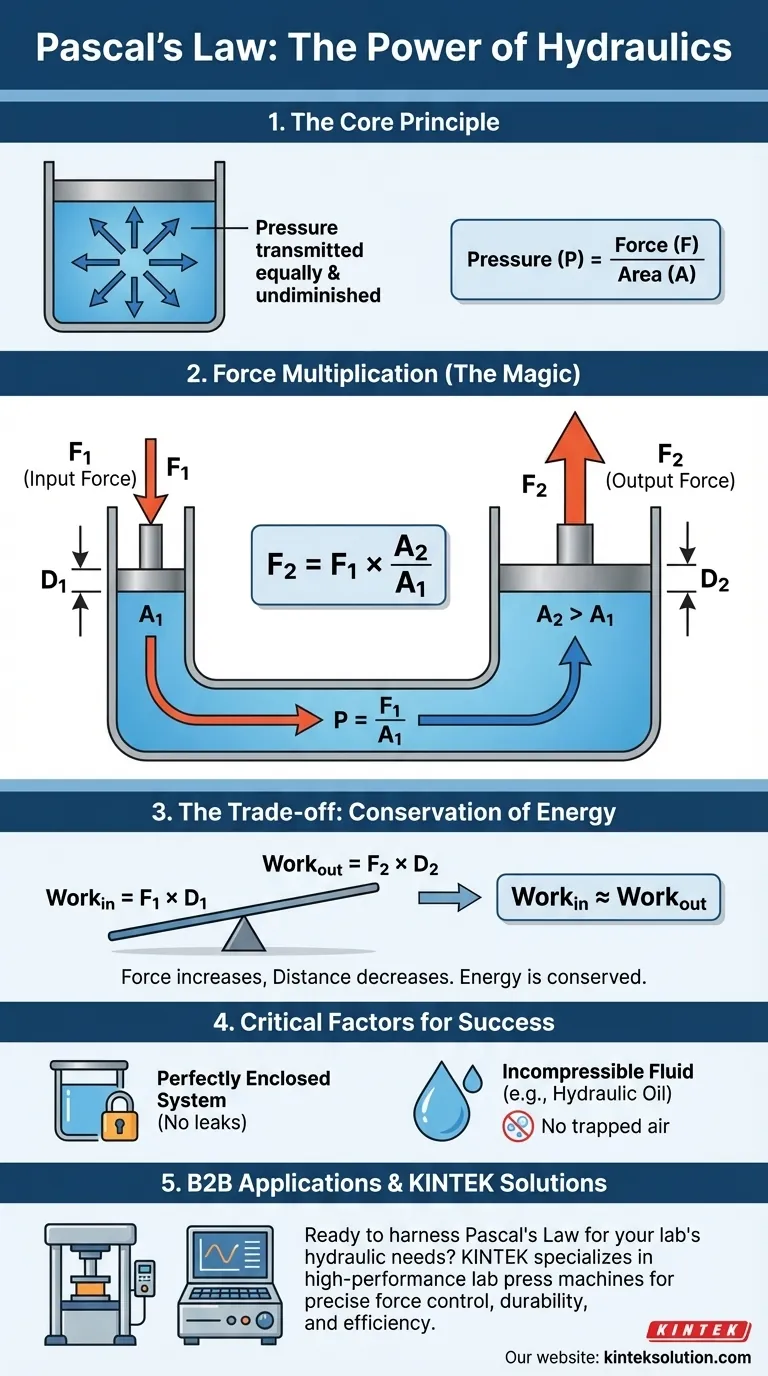
Productos relacionados
- Prensa hidráulica automática de laboratorio para prensado de pellets XRF y KBR
- Prensa hidráulica de laboratorio manual calentada con placas calientes integradas Máquina prensa hidráulica
- Máquina automática de prensar hidráulica calentada con placas calientes para laboratorio
- Prensas hidráulicas automáticas con placas calefactadas para laboratorio
- Prensa hidráulica de laboratorio Máquina de prensa de pellets para guantera
La gente también pregunta
- ¿Cómo se comparan los pellets prensados con otros métodos de preparación de muestras para análisis de XRF? Mejore la precisión y eficiencia en su laboratorio
- ¿Cuáles son los beneficios de prensar muestras en pastillas para el análisis de FRX? Aumente la precisión y la reproducibilidad
- ¿Cuál es el propósito de crear pastillas para la espectroscopía XRF utilizando una prensa hidráulica? Garantizar un análisis elemental preciso y reproducible
- ¿Por qué es importante una prensa hidráulica para la espectroscopia FTIR? Asegure un análisis preciso de muestras con pastillas de KBr
- ¿Cómo garantizan las prensas hidráulicas la precisión y la uniformidad en la aplicación de presión?Consiga un control fiable de la fuerza para su laboratorio
